光照原理

现实世界中的物体被光线照射时,会反射一部分 光。只有当反射光线进人你的眼睛时， 你才能够看到物体并辩认出它的颜色。比如，白色的盒子会反射白光，当白光进入你的 眼睛时，你才能看到盒子是白色的。 在现实世界中，当光线照射到物体上时，发生了两个重要的现象(见图8.1) :

• 根据光源和光线方向，物体不同表面的明暗程度变得不一-致。
• 根据光源和光线方向，物体向地面投下了影子。.

在三维图形学中术语着色(shading) 的真正含义就是，根据光照条件重建“物体各表 面明暗不一的效果”的过程。物体向地面投下影子的现象，又被称为阴影(shadowing)。 在讨论着色过程之前，考虑两件事:

• 发出光线的光源的类型。
• 物体表面如何反射光线。

光源类型

当物体被光线照射时，必然存在发出光线的光源。真实世界中的光主要有两种类型:

• 平行光(directional light)，类似于自然中的太阳光;

• 点光源光(point light) ,类似于人造灯泡的光；

• 环境光(ambient light) 来模拟真实世界中的非直射光( 也就是由光源发出后经过墙壁或其他物体反射后的光)

• 聚光灯光(spot light) 来模拟电筒、车前灯等。

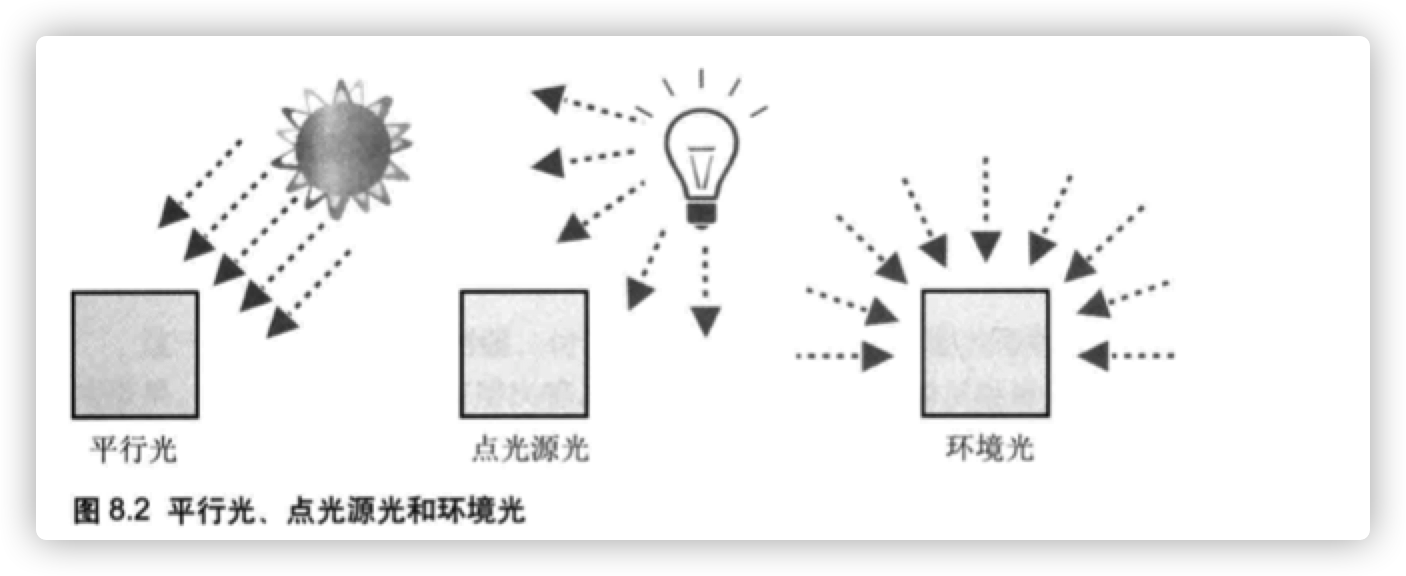
• 平行光:顾名思义，平行光的光线是相互平行的，平行光具有方向。平行光可以看作是无限远处的光源(比如太阳)发出的光。因为太阳距离地球很远，所以阳光到达地球时可以认为是平行的。平行光很简单，可以用一个方向和一个颜色来定义。

• 点光源光:点光源光是从一个点向周围的所有方向发出的光。点光源光可以用来表示现实中的灯泡、火焰等。我们需要指定点光源的位置和颜色'。光线的方向将根据点光源的位置和被照射之处的位置计算出来，因为点光源的光线的方向在场景内的不同位置是不同的。

• 环境光:环境光(间接光)是指那些经光源(点光源或平行光源)发出后，被墙壁等物体多次反射，然后照到物体表面上的光。环境光从各个角度照射物体，其强度都是致的4比如说，在夜间打开冰箱的门,整个厨房都会有些微微亮,这就是环境光的作用。 环境光不用指定位置和方向，只需要指定颜色即可。

反射类型

物体向哪个方向反射光，反射的光是什么颜色，取决于以下两个因素：

• 入射光，入射光的信息包括入射光的方向和颜色
• 物体表面的类型，物体表面的信息包括表面的固有颜色(也称基底色)和反射特性。 物体表面反射光线的方式有两种:
• 漫反射(diffuse reflection)
• 环境反射(enviroment/ambient reflection)。本节的重点是如何根据上述两种信息(入射光和物体表面特性)来计算出反射光的颜色。

漫反射

漫反射是针对平行光或点光源而言的。漫反射的反射光在各个方向上是均匀的，如 图8.3所示。如果物体表面像镜子一样光滑，那么光线就会以特定的角度反射出去;但 是现实中的大部分材质，比如纸张、岩石、塑料等，其表面都是粗糙的，在这种情况下 反射光就会以不固定的角度反射出去。漫反射就是针对后一种情况而建立的理想反射模型。

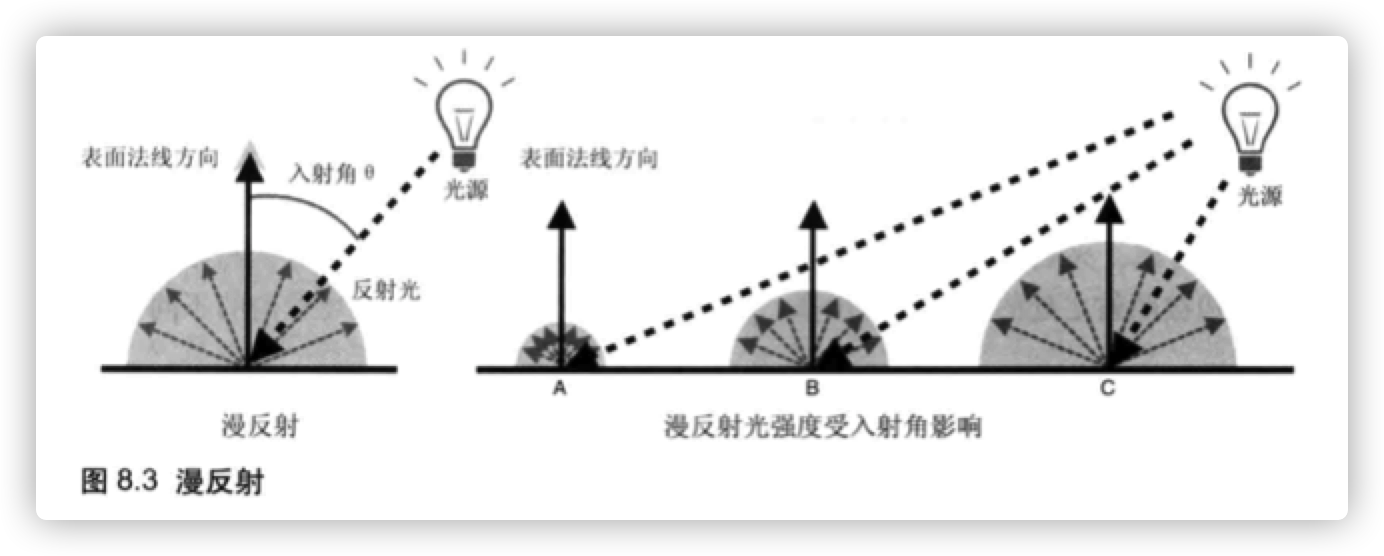
在漫反射中，反射光的颜色取决于入射光的颜色、表面的基底色、入射光与表面形 成的入射角。我们将入射角定义为入射光与表面的法线形成的夹角，并用θ表示，那么漫反射光的颜色可以根据下式计算得到:

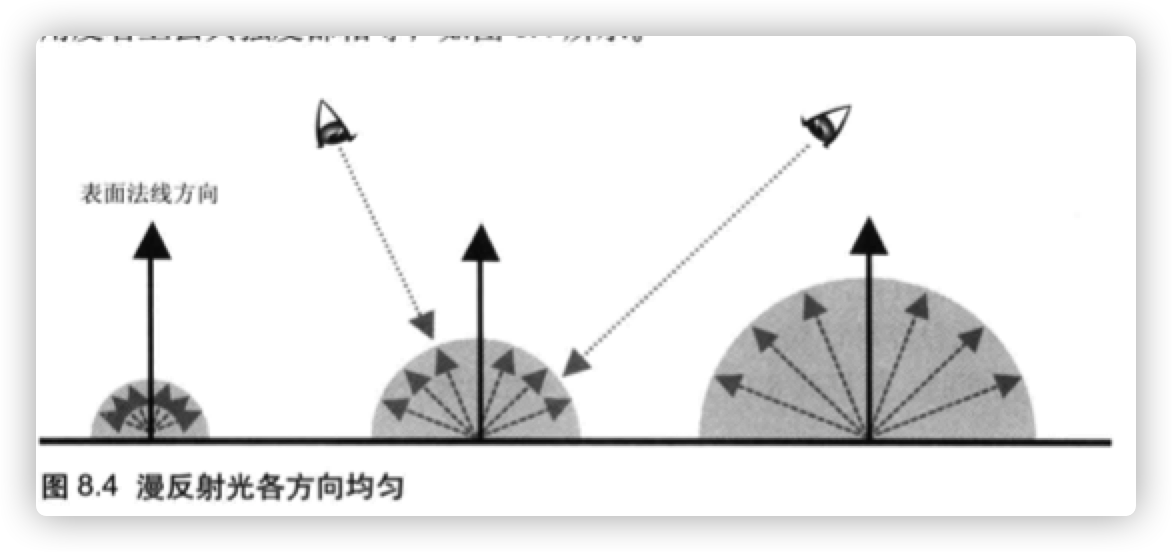
式子中，入射光颜色指的是点光源或平行光的颜色，乘法操作是在颜色矢量上 逐分量(R, G、B)进行的。因为漫反射光在各个方向上都是“均匀”的，所以从任何角度看上去其强度都相等，如图8.4所示。

环境反射

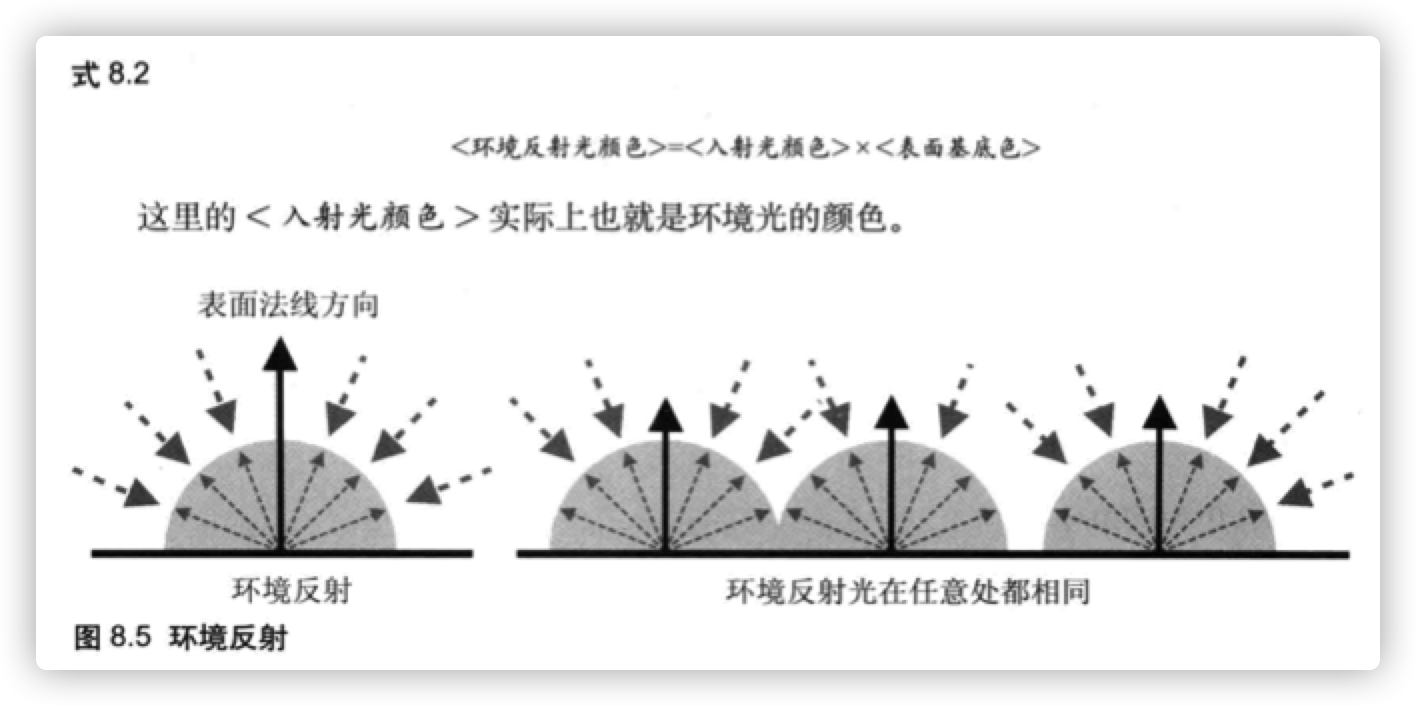
环境反射是针对环境光而言的。在环境反射中，反射光的方向可以认为就是人射光的反方向。由于环境光照射物体的方式就是各方向均匀、强度相等的，所以反射光也是 各向均匀的，如图8.5所示。我们可以这样来描述它:

根据光线和表面的方向计算入射角

在程序中，我们没法像前一节最后那样，直接说“人射角θ是多少多少度"。我们 必须根据人射光的方向和物体表面的朝向(即法线方向)来计算出人射角。这并不简单， 因为在创建三维模型的时候，我们无法预先确定光线将以怎样的角度照射到每个表面上。 但是，我们可以确定每个表面的朝向。在指定光源的时候，再确定光的方向，就可以用 这两项信息来计算出人射角了。 幸运的是，我们可以通过计算两个矢量的点积，来计算这两个矢量的夹角余弦值 cos θ。。点积运算的使用非常频繁,GLSL ES内置了点积运算函数(详见附录B)。在公式中， 我们使用点符号，来表示点积运算。这样，cosθ就可以通过下式计算出来:

法线:表面的朝向

物体表面的朝向，即垂直于表面的方向，又称法线或法向量。法向量有三个分量，向量(nx, ny, nz)表示从原点(0, 0, 0)指向点(nx, ny, nz)的方向。 比如说，向量(1,0,0) 表示x轴正方向，向量(0,0, 1)表示z轴正方向。涉及到表面和法向量的问题时，必须考虑以下两点:

一个表面具有两个法向量

每个表面都有两个面，“正面” 和“背面"。两个面各自具有一个法向量。比如，垂 直于z轴的x-y平面，其背面的法向量为x正半轴，即(0,0, 1)，如图8.7 (左)所示; 而背面的法向量为x负半轴，即(0,0,-1), 如图8.7 (右)所示。

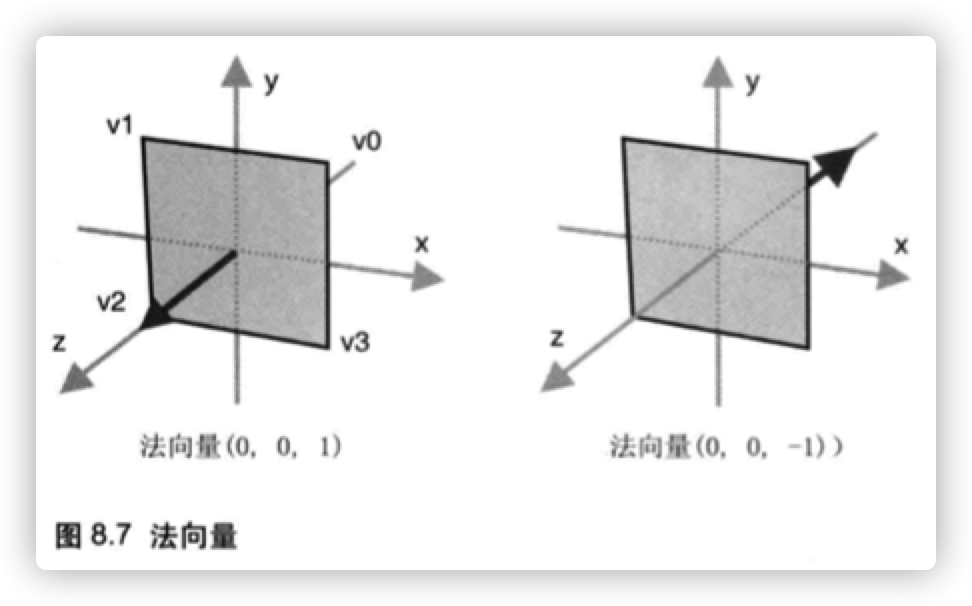
平面的法向量唯一

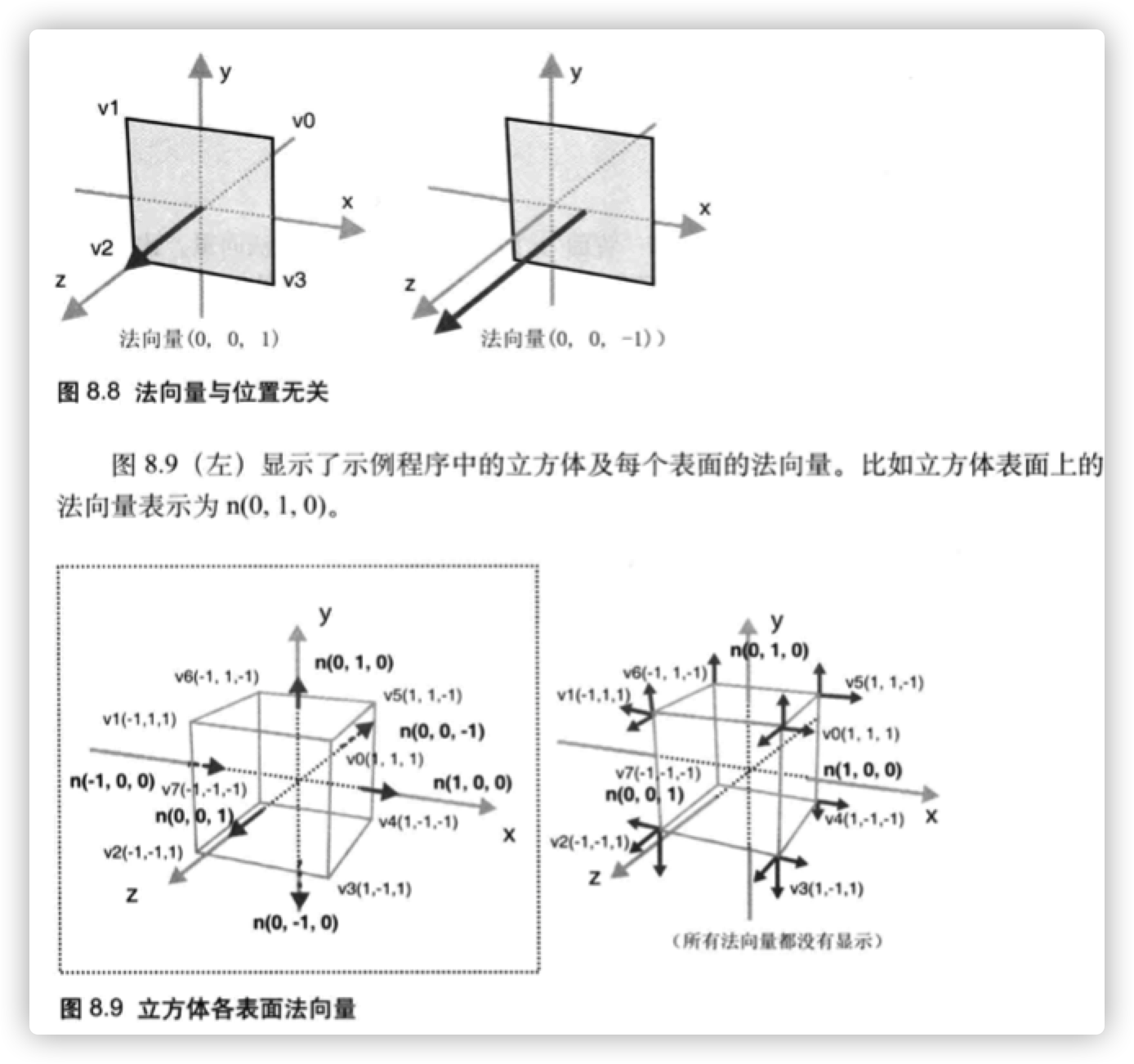
由于法向量表示的是方向，与位置无关，所以一个平面只有一个法向量。换句话说， 平面的任意一点都具有相同的法向量。 进一步来说，即使有两个不同的平面，只要其朝向相同(也就是两个平面平行)，法 向量也相同。比方说，有一个经过点(10, 98, 9)的平面，只要它垂直于z轴，它的法向 量仍然是(0,0, 1)和(0,0,-1),和经过原点并垂直于z轴的平面一样，如图8.8所示。

attribute vec4 a_Position;
attribute vec4 a_Color;
//法向量
attribute vec4 a_Normal;

uniform mat4 u_MvpMatrix;
//光照颜色
uniform vec3 u_LightColor;
//光照方向 （归一化）
uniform vec3 u_LightDirection;

varying vec4 v_Color;

void main(){
    gl_Position = u_MvpMatrix * a_Position;
    //    对法向量归一化
    vec3 normal = normalize(vec3(a_Normal));
    //    计算光线方向和法向量的点积，算出 cosθ。
    //\vec{a} \cdot \vec{b} = |\vec{a}| \, |\vec{b}| \cos \theta \;
    //    cosθ = 光线方向 * 法线方向
    float nDotL = max(dot(u_LightDirection, normal), 0.0);

    //    漫反射光颜色 = 入射光颜色 * 表面基底色 * cosθ
    vec3 diffuse = u_LightColor * vec3(a_Color) * nDotL;

    v_Color = vec4(diffuse, a_Color.a);
}