运动物体的光照效果

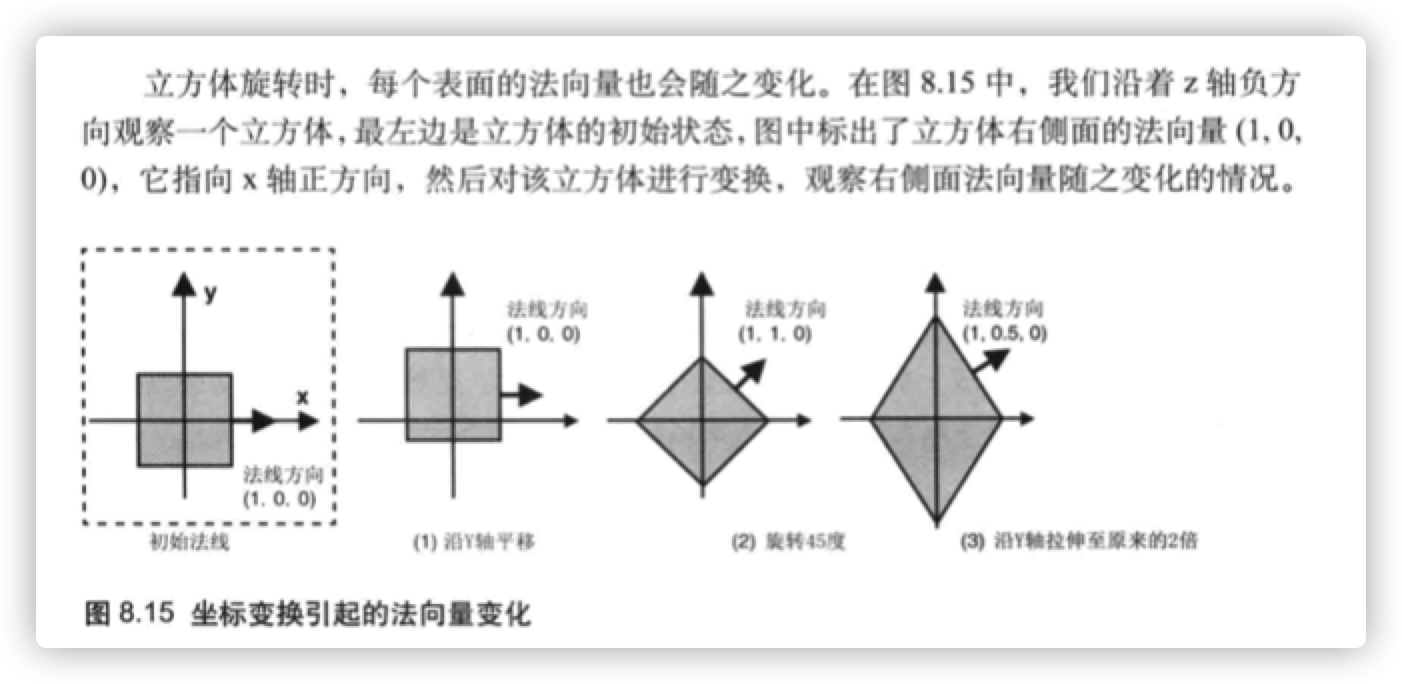
• 平移变换不会改变法向量，因为平移不会改变物体的方向。
• 旋转变换会改变法向量，因为旋转改变了物体的方向。
• 缩放变换对法向量的影响较为复杂。如你所见，最右侧的图显示了立方体先旋转了45度，再在y轴上拉伸至原来的2倍的情况。此时法向量改变了，因为表面的朝向改变了。但是，如果缩放比例在所有的轴上都-致的话，那么法向量就不会变化。最后,即使物体在某些轴上的缩放比例并不一-致, 法向量也并不一-定 会变化，比如将最左侧图中的立方体在y轴方向上拉伸两倍，法向量就不会变化。

显然,在对物体进行不同变换时,法向量的变化情况较为复杂(特别是缩放变换时)。 这时候，数学公式就会派上用场了。

魔法矩阵:逆转置矩阵

在第4章中曾讨论过，对顶点进行变换的矩阵称为模型矩阵。如何计算变换之后的法向量呢? 只要将变换之前的**法向量乘以模型矩阵的逆转置矩阵(inversetransposematrix)**即可。 所谓逆转置矩阵，就是逆矩阵的转置。

逆矩阵的含义是,如果矩阵M的逆矩阵是R,那么R*M或M*R的结果都是单位矩阵。 转置的意思是，将矩阵的行列进行调换(看上去就像是沿着左.上-右下对角线进行了翻转)。

更详细的内容参见附录E“逆转置矩阵"。这里将逆转置矩阵的用法总结如下:

规则:用法向量乘以模型矩阵的逆转置矩阵，就可以求得变换后的法向量。

求逆转值矩阵的两个步骤:

1. 求原矩阵的逆矩阵。
2. 将上一步求得的逆矩阵进行转置。